一.解决几何最值问题的通常思路
两点之间线段最短;
直线外一点与直线上所有点的连线段中,垂线段最短;
三角形两边之和大于第三边或三角形两边之差小于第三边(重合时取到最值)
是解决几何最值问题的理论依据,根据不同特征转化是解决最值问题的关键.通过转化减少变量,向三个定理靠拢进而解决问题;直接调用基本模型也是解决几何最值问题的高效手段。
几何最值问题中的基本模型举例:


二、典型题型
1.如图:点P是∠AOB内一定点,点M、N分别在边OA、OB上运动,若∠AOB=45°,OP=图片,则△PMN的周长的最小值为 .
图片
【分析】作P关于OA,OB的对称点C,D.连接OC,OD.则当M,N是CD与OA,OB的交点时,△PMN的周长最短,最短的值是CD的长.根据对称的性质可以证得:△COD是等腰直角三角形,据此即可求解.
【解答】解:作P关于OA,OB的对称点C,D.连接OC,OD.则当M,N是CD与OA,OB的交点时,△PMN的周长最短,最短的值是CD的长.
∵PC关于OA对称,
∴∠COP=2∠AOP,OC=OP
同理,∠DOP=2∠BOP,OP=OD
∴∠COD=∠COP+∠DOP=2(∠AOP+∠BOP)=2∠AOB=90°,OC=OD.
∴△COD是等腰直角三角形.
则CD=图片OC=图片×3图片=6.

【题后思考】本题考查了对称的性质,正确作出图形,理解△PMN周长最小的条件是解题的关键.
2.如图,当四边形PABN的周长最小时,a= .

【分析】因为AB,PN的长度都是固定的,所以求出PA+NB的长度就行了.问题就是PA+NB什么时候最短.
把B点向左平移2个单位到B′点;作B′关于x轴的对称点B″,连接AB″,交x轴于P,从而确定N点位置,此时PA+NB最短.
设直线AB″的解析式为y=kx+b,待定系数法求直线解析式.即可求得a的值.
【解答】解:将N点向左平移2单位与P重合,点B向左平移2单位到B′(2,﹣1),
作B′关于x轴的对称点B″,根据作法知点B″(2,1),
设直线AB″的解析式为y=kx+b,
则图片,解得k=4,b=﹣7.
∴y=4x﹣7.当y=0时,x=图片,即P(图片,0),a=图片.
故答案填:图片.

【题后思考】考查关于X轴的对称点,两点之间线段最短等知识.
3.如图,A、B两点在直线的两侧,点A到直线的距离AM=4,点B到直线的距离BN=1,且MN=4,P为直线上的动点,|PA﹣PB|的最大值为 .

【分析】作点B于直线l的对称点B′,则PB=PB′因而|PA﹣PB|=|PA﹣PB′|,则当A,B′、P在一条直线上时,|PA﹣PB|的值最大.根据平行线分线段定理即可求得PN和PM的值然后根据勾股定理求得PA、PB′的值,进而求得|PA﹣PB|的最大值.
【解答】解:作点B于直线l的对称点B′,连AB′并延长交直线l于P.
∴B′N=BN=1,
过D点作B′D⊥AM,
利用勾股定理求出AB′=5
∴|PA﹣PB|的最大值=5.
【题后思考】本题考查了作图﹣轴对称变换,勾股定理等,熟知“两点之间线段最短”是解答此题的关键.
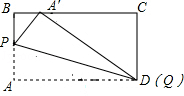
4.动手操作:在矩形纸片ABCD中,AB=3,AD=5.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点A′在BC边上可移动的最大距离为 .
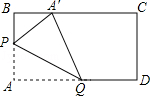
【分析】本题关键在于找到两个极端,即BA′取最大或最小值时,点P或Q的位置.经实验不难发现,分别求出点P与B重合时,BA′取最大值3和当点Q与D重合时,BA′的最小值1.所以可求点A′在BC边上移动的最大距离为2.
【解答】解:当点P与B重合时,BA′取最大值是3,
当点Q与D重合时(如图),由勾股定理得A′C=4,此时BA′取最小值为1.
则点A′在BC边上移动的最大距离为3﹣1=2.
故答案为:2
【题后思考】本题考查了学生的动手能力及图形的折叠、勾股定理的应用等知识,难度稍大,学生主要缺乏动手操作习惯,单凭想象造成错误.
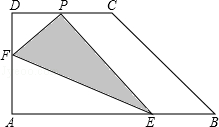
5.如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.当P落在直角梯形ABCD内部时,PD的最小值等于 .
【分析】如图,经分析、探究,只有当直径EF最大,且点A落在BD上时,PD最小;根据勾股定理求出BD的长度,问题即可解决.
【解答】解:如图,
∵当点P落在梯形的内部时,∠P=∠A=90°,
∴四边形PFAE是以EF为直径的圆内接四边形,
∴只有当直径EF最大,且点A落在BD上时,PD最小,
此时E与点B重合;
由题意得:PE=AB=8,
由勾股定理得:
BD2=82+62=80,
∴BD=图片,
∴PD=图片.
【题后思考】该命题以直角梯形为载体,以翻折变换为方法,以考查全等三角形的判定及其性质的应用为核心构造而成;解题的关键是抓住图形在运动过程中的某一瞬间,动中求静,以静制动.



